Zadanie
dodane przez
monika2433
,
18.04.2012 15:00
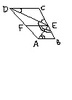
Dany jest czworokąt ABCD, w którym AB || CD. Na boku BC wybrano taki punkt E, że | EC| = |CD| i |EB| = |BA|. Wykaż, że kąt AED jest prosty.
Nadesłane rozwiązania ( 2 )
Rozwiązanie 1
dodane przez
AnnaS
,
04.05.2012 13:45
EF || AB, zatem kąt BAE = kątowi FEA. Tak samo kąt FED = kątowi CDE. Jednocześnie EC = DC, więc kąt CDE = kątowi CED. Analogicznie kąt BAE = kątowi BEA. Zatem kąt BEC = 2*AEF + 2*FED = 180°. Wystarczy podzielic przez 2 i gotowe
-
- Dodaj komentarz
Musisz się
zalogować
aby dodać komentarz
Rozwiązanie 2
dodane przez
AnnaS
,
05.05.2012 18:56
Można też inaczej:
Kąty DCE i ABE dopełniają się do (DCE + ABE =
(DCE + ABE =  ).
).
Jednocześnie DCE = - 2*DEC, a ABE =
- 2*DEC, a ABE =  - 2*AEB.
- 2*AEB.
Podstawiając to do pierwszego:
 - 2*DEC +
- 2*DEC +  - 2*AEB =
- 2*AEB =  / -
/ -
-2*DEC -2*AEB + = 0
= 0
2(DEC + AEB) =
DEC + AEB =
Jednocześnie: DEC + AEB + DEA =
 + DEA =
+ DEA = 
DEA =
Co należało wykazać :)
Powodzenia na maturze!
Kąty DCE i ABE dopełniają się do
 (DCE + ABE =
(DCE + ABE =  ).
).
Jednocześnie DCE =
 - 2*DEC, a ABE =
- 2*DEC, a ABE =  - 2*AEB.
- 2*AEB.
Podstawiając to do pierwszego:
 - 2*DEC +
- 2*DEC +  - 2*AEB =
- 2*AEB =  / -
/ -
-2*DEC -2*AEB +
 = 0
= 0
2(DEC + AEB) =

DEC + AEB =

Jednocześnie: DEC + AEB + DEA =

 + DEA =
+ DEA = 
DEA =

Co należało wykazać :)
Powodzenia na maturze!
Musisz się
zalogować
aby dodać komentarz


COMMENT_CONTENT