Zadanie
dodane przez
Ania_M
,
17.09.2012 13:58
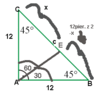
Ramię trójkąta równoramiennego ma długość 12 i tworzy z podstawą kąt o mierze 45 stopni.Z wierzchołka tego trójkąta poprowadzono do podstawy odcinek dzielący kąt przy wierzchołku w stosunku 2:1. Oblicz pola powstałych trójkątów.
Nadesłane rozwiązania ( 1 )
Rozwiązanie 1
dodane przez
memory10
,
19.09.2012 17:37
 +
+  =
= 
288=

c=12

Pabc= 12*12/2 = 72
Pabc= Paec + Pabe
Paec=
 *|AC| * |EC| * sin
*|AC| * |EC| * sin  = 1/2 *12* x*
= 1/2 *12* x*  /2
/2
Pabe = 1/2 * |AB| *|BE| * sin
 = 1/2 *12 *(12
= 1/2 *12 *(12  - x) *
- x) *  /2
/2
skala podobieństwa : 2/1 czyli skala pod. pól : 4/1 =>
3
 * x / 3
* x / 3 *(12
*(12  - x) = 4/1
- x) = 4/1
312 *(12
 - x) * x =288 -12
- x) * x =288 -12  *x
*x
x= 48
 /5
/5
Paec=57,6
Pabe=14,4
-
- Dodaj komentarz
Musisz się
zalogować
aby dodać komentarz


COMMENT_CONTENT