Zadanie
dodane przez
sinus
,
06.10.2012 15:59
Proszę o pomoc
Pole kwadratu, którego przekatna jest o 2 cm dłuzsza od boku, jest równe:
a).2( + 1)cm^
+ 1)cm^
b). ( 12 + 8 ) cm^
) cm^
c). cm
cm
d). ( + 1) cm^
+ 1) cm^
Bardzo dziękuję
Pole kwadratu, którego przekatna jest o 2 cm dłuzsza od boku, jest równe:
a).2(
 + 1)cm^
+ 1)cm^
b). ( 12 + 8
 ) cm^
) cm^
c).
 cm
cm
d). (
 + 1) cm^
+ 1) cm^
Bardzo dziękuję
Nadesłane rozwiązania ( 1 )
Rozwiązanie 1
dodane przez
konto-usuniete
,
07.10.2012 20:13
a - długość boku kwadratu
a + 2 = d - długość przekątnej kwadratu
* wszystko jest w centymetrach; omijam jednostki żeby opis był bardziej czytelny
z własności trójkąta o kątach ,
,  ,
,  ( bo jak poprowadzimy w trójkącie przekątną to nam wyjdą dwa trójkąty o wyżej wymienionych kątach) wiemy, że jeśli kwadrat ma bok o długości a, to jego przekątna ma długość a
( bo jak poprowadzimy w trójkącie przekątną to nam wyjdą dwa trójkąty o wyżej wymienionych kątach) wiemy, że jeśli kwadrat ma bok o długości a, to jego przekątna ma długość a 
Więc
a + 2 = a
a po przekształceniach powyższej równości (na zdjęciu) wychodzi, że:
a = 2 + 2
+ 2
Teraz do wzoru P =
P =^{2}})
P = (12 + 8 )
) 
Odp.: B.
a + 2 = d - długość przekątnej kwadratu
* wszystko jest w centymetrach; omijam jednostki żeby opis był bardziej czytelny
z własności trójkąta o kątach
 ,
,  ,
,  ( bo jak poprowadzimy w trójkącie przekątną to nam wyjdą dwa trójkąty o wyżej wymienionych kątach) wiemy, że jeśli kwadrat ma bok o długości a, to jego przekątna ma długość a
( bo jak poprowadzimy w trójkącie przekątną to nam wyjdą dwa trójkąty o wyżej wymienionych kątach) wiemy, że jeśli kwadrat ma bok o długości a, to jego przekątna ma długość a 
Więc
a + 2 = a

a po przekształceniach powyższej równości (na zdjęciu) wychodzi, że:
a = 2
 + 2
+ 2
Teraz do wzoru P =

P =
^{2}})
P = (12 + 8
 )
) 
Odp.: B.
-
- Dodaj komentarz
Musisz się
zalogować
aby dodać komentarz
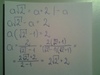


COMMENT_CONTENT