BARDZO PROSZĘ , o podanie odpowiedzi i pokazać jak się to rozwiązuję. Będe bardzo wdzięczna z góry dziękuję. W trapezie równoramiennym kąt ostry wynosi $30^{\circ}$ . Ramię ma długość b cm i jest równe odcinkowi łączącemu środki ramion trapezu. Pole powierzchni trapezu wynosi: A. $\sqrt{3}$ $b^{2}$ cm kwadrat. B. $b^{2}$ cm kwadrat C. $\frac{1}{2}$ $b^{2}$ cm kwadrat D. ( $\sqrt{3}$ -1) $b^{2}$ cm kwadrat

Zadanie dodane przez zxcv94 , 04.11.2012 11:37

BARDZO PROSZĘ , o podanie odpowiedzi i pokazać jak się to rozwiązuję. Będe bardzo wdzięczna z góry dziękuję.

W trapezie równoramiennym kąt ostry wynosi $30^{\circ}$ . Ramię ma długość b cm i jest równe odcinkowi łączącemu środki ramion trapezu. Pole powierzchni trapezu wynosi:
A. $\sqrt{3}$ $b^{2}$ cm kwadrat.
B. $b^{2}$ cm kwadrat
C. $\frac{1}{2}$ $b^{2}$ cm kwadrat
D. ( $\sqrt{3}$ -1) $b^{2}$ cm kwadrat

Nadesłane rozwiązania ( 1 )

Rozwiązanie 1 dodane przez monijatcz , 04.11.2012 11:55

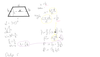
Załącznik- rozwiązanie z rysunkiem.
Oznaczamy podstawy trapezu jako c i d zaś ramię jako b cm.
Korzystamy ze wzoru na odcinek łączący środki ramion trapezu ( połowa sumy podstaw)
Korzystamy z funkcji sinus by wyznaczyć h.

Dodaj komentarz

Znasz inny sposób na rozwiązanie tego zadania?

Dodaj swoje rozwiązanie

Ekspresowy Kurs Maturalny z matematyki

Nadesłane rozwiązania ( 1 )

Znasz inny sposób na rozwiązanie tego zadania?

Dodaj swoje rozwiązanie: