Zadanie
dodane przez
zxcv94
,
13.11.2012 07:54
BARDZO PROSZĘ , o podanie odpowiedzi i pokazać jak się to rozwiązuję. Będe bardzo wdzięczna z góry dziękuję.
Na przeciwprostokątnej Ab trójkąta prostokątnego ABC wybrano punkty D i E w taki sposób, by AC=AE oraz BC=BD. Udowodnij, że kąt DCE=
Na przeciwprostokątnej Ab trójkąta prostokątnego ABC wybrano punkty D i E w taki sposób, by AC=AE oraz BC=BD. Udowodnij, że kąt DCE=

Nadesłane rozwiązania ( 1 )
Rozwiązanie 1
dodane przez
monijatcz
,
13.11.2012 22:28
Załącznik
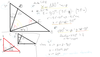
Z rysunku1 wynika, że otrzymujemy trójkąt równoramienny ACE. więc kąty prz boku CE są równe. oznaczyłam je jako , zaś kąt ECB=
, zaś kąt ECB=
Z rysunku2 wynika, że otrzymujemy trójkąt równoramienny BCD. więc kąty prz boku CD są równe. oznaczyłam je jako , zaś kąt ACD=
, zaś kąt ACD=
Połączyłam oba rysunki i powstał rysunek 3 , w którym kąt DCE oznaczyłam jako
Z trójkąta DCE wyznaczyłam (podpunkt4)
(podpunkt4)
Następnie z kąta ACB wyznaczyłam . (podpunkt5)
. (podpunkt5)
Porównałam otrzymane wyniki dla kąta gamma . (podpunkt6)
Otrzymany wynik podstawiłam do wyniku z podpunktu5) i wyszło, że gamma wynosi
koniec
Z rysunku1 wynika, że otrzymujemy trójkąt równoramienny ACE. więc kąty prz boku CE są równe. oznaczyłam je jako
 , zaś kąt ECB=
, zaś kąt ECB=
Z rysunku2 wynika, że otrzymujemy trójkąt równoramienny BCD. więc kąty prz boku CD są równe. oznaczyłam je jako
 , zaś kąt ACD=
, zaś kąt ACD=
Połączyłam oba rysunki i powstał rysunek 3 , w którym kąt DCE oznaczyłam jako

Z trójkąta DCE wyznaczyłam
 (podpunkt4)
(podpunkt4)
Następnie z kąta ACB wyznaczyłam
 . (podpunkt5)
. (podpunkt5)
Porównałam otrzymane wyniki dla kąta gamma . (podpunkt6)
Otrzymany wynik podstawiłam do wyniku z podpunktu5) i wyszło, że gamma wynosi

koniec
-
- Dodaj komentarz
Musisz się
zalogować
aby dodać komentarz


COMMENT_CONTENT