Zadanie
dodane przez
aga4804
,
19.09.2013 12:42
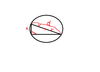
1.26. W okrąg o promieniu 5 wpisano trójkąt prostokątny. Oblicz pole P tego trójkąta, gdy cosinus jednego z kątów ostrych jest równy 1/3.
Nadesłane rozwiązania ( 1 )
Rozwiązanie 1
dodane przez
anuuila
,
19.09.2013 13:33
1) najpierw wyknaj rysunek
2) ponieważ wpisano trójkąt prostokątny wiemy ze jego przeciwprostokątna ma długość
3) wiemy ze a u nas
a u nas 
4) porównujemy i rozwiązujemy równanie



5) twierdzenie pitagorasa i dlugość dostaniesz dlugość drugiego boku y

6) pole liczysz ze wzoru

2) ponieważ wpisano trójkąt prostokątny wiemy ze jego przeciwprostokątna ma długość

3) wiemy ze
 a u nas
a u nas 
4) porównujemy i rozwiązujemy równanie



5) twierdzenie pitagorasa i dlugość dostaniesz dlugość drugiego boku y

6) pole liczysz ze wzoru

-
- Dodaj komentarz
Musisz się
zalogować
aby dodać komentarz


COMMENT_CONTENT