Trójkąt prostokątny o przyprostokątnych długości 3 cm i 9 cm obraca się dookoła krótszego boku Oblicz objętość i pole powierzchni otrzymanej bryły.

Zadanie dodane przez netka75 , 11.01.2013 20:19

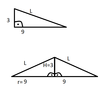
Trójkąt prostokątny o przyprostokątnych długości 3 cm i 9 cm obraca się dookoła

krótszego boku

Oblicz objętość i pole powierzchni otrzymanej bryły.

Nadesłane rozwiązania ( 1 )

Rozwiązanie 1 dodane przez kasienka1813 , 12.01.2013 12:22

r=9cm
H=3cm
Pp=pi* $r^{2}$
Pp= $9^{2}$ * pi= 81pi $cm^{2}$
objętość V= 1/3 Pp *H=1/3* 81pi $cm^{2}$ *3cm=81 81pi $cm^{3}$ pi

Pole powierzchni całkowitej Pc=pi*r(r+L)
naszym l jest przeciwprostokątna trójkąta którą wyliczymy z Pitagorasa:

$3^{2}$ + $9^{2}$ = $L^{2}$
9+81= $L^{2}$
90= $L^{2}$
L= $\sqrt{90}=3$ \sqrt{10}

Pc=pi*9cm(9+3 $\sqrt{10})=81cmPi+27$ \sqrt{10}cmpi

Dodaj komentarz

Znasz inny sposób na rozwiązanie tego zadania?

Dodaj swoje rozwiązanie

Trójkąt prostokątny o przyprostokątnych długości 3 cm i 9 cm obraca się dookoła krótszego boku Oblicz objętość i pole powierzchni otrzymanej bryły.

Ekspresowy Kurs Maturalny z matematyki

Nadesłane rozwiązania ( 1 )

Znasz inny sposób na rozwiązanie tego zadania?

Dodaj swoje rozwiązanie: