Oblicz pole i obwód trójkąta prostokątnego, w którym jedna przyprostokątna ma długość 5cm, a wysokość opuszczona z wierzchołka kąta prostego ma długość 3cm. Zadanie ma być na kartce rozwiązania P=9$\frac{3}{8}$ obw=15 cm

Zadanie dodane przez niki1234 , 24.05.2013 08:36

Oblicz pole i obwód trójkąta prostokątnego, w którym jedna przyprostokątna ma długość 5cm, a wysokość opuszczona z wierzchołka kąta prostego ma długość 3cm.

Zadanie ma być na kartce

rozwiązania
P=9 $\frac{3}{8}$
obw=15 cm

Nadesłane rozwiązania ( 1 )

Rozwiązanie 1 dodane przez Science4U , 24.05.2013 09:59

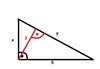
W załączniku znajduje się odpowiedni rysunek. Zgodnie z tym rysunkiem można ułożyć następujący układ równań:

$\left \{ \begin{array}{l}x^2+5^2=y^2\\[0.1cm]\cfrac{5* x}{2}=\cfrac{y* 3}{2}\end{array}\right .$

Wykorzystałam tw. Pitagorasa oraz zapisałam pole tego trójkąta na dwa sposoby. Oto rozwiązanie tego układu:

$\left \{ \begin{array}{l}x^2+25=y^2\\[0.1cm]5x=3y\end{array}\right .$

$\left \{ \begin{array}{l}x^2=y^2-25\\[0.1cm]y=\cfrac{5}{3}x\end{array}\right .$

Zależność z drugiego równania podstawiam do pierwszego równania:

$x^2=\left ( \cfrac{5}{3}x\right ) ^2-25$

$x^2=\cfrac{25}{9}x^2-25$

$x^2-\cfrac{25}{9}x^2=-25$

$-\cfrac{16}{9}x^2=-25$

$\cfrac{16}{9}x^2=25$

$\cfrac{4}{3}x=5$

$x=\cfrac{15}{4}$

$y=\cfrac{5}{3}* \cfrac{15}{4}$

$y=\cfrac{25}{4}$

Zatem pole tego trójkąta to:

$P=\cfrac{5* x}{2}$

$P=\cfrac{5* \cfrac{15}{4}}{2}$

$P=\cfrac{75}{8}$

$P=9\cfrac{3}{8}$

Obwód tego trójkąta to:

$Obw=5+x+y$

$Obw=5+\cfrac{15}{4}+\cfrac{25}{4}$

$Obw=5+\cfrac{40}{4}$

$Obw=15$

Dodaj komentarz

Znasz inny sposób na rozwiązanie tego zadania?

Dodaj swoje rozwiązanie

Oblicz pole i obwód trójkąta prostokątnego, w którym jedna przyprostokątna ma długość 5cm, a wysokość opuszczona z wierzchołka kąta prostego ma długość 3cm. Zadanie ma być na kartce rozwiązania P=9$\frac{3}{8}$ obw=15 cm

Ekspresowy Kurs Maturalny z matematyki

Nadesłane rozwiązania ( 1 )

Znasz inny sposób na rozwiązanie tego zadania?

Dodaj swoje rozwiązanie: