Oblicz pole powierzchni ostrosłupa prawidłowego czworokątnego , którego krawędź podstawy ma długość a, a krawędź boczna b..

Zadanie dodane przez SYLWUCHA13 , 02.04.2014 12:34

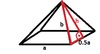
Oblicz pole powierzchni ostrosłupa prawidłowego czworokątnego , którego
krawędź podstawy ma długość a, a krawędź boczna b..

Nadesłane rozwiązania ( 1 )

Rozwiązanie 1 dodane przez Science4U , 05.04.2014 16:48

Ostrosłup prawidłowy czworokątny ma w podstawie kwadrat, a ściany boczne są przystającymi trójkątami równoramiennymi. Zobacz rysunek w załączniku.

$P_c=P_p+P_b$

$P_p=a^2$

$P_b=4* \cfrac{a* h}{2}$

$P_b=2ah$

Wysokość ściany bocznej można obliczyć, korzystając z twierdzenie Pitagorasa, a więc:

$h^2+\cfrac{1}{4}a^2=b^2$

$h=\sqrt{b^2-\cfrac{a^2}{4}}$

$h=\cfrac{\sqrt{4b^2-a^2}}{2}$

Zatem powierzchnia boczna wyraża się wzorem:

$P_b=a\sqrt{4b^2-a^2}$

Podsumowując:

$P_c=a^2+a\sqrt{4b^2-a^2}$

Dodaj komentarz

Znasz inny sposób na rozwiązanie tego zadania?

Dodaj swoje rozwiązanie

Oblicz pole powierzchni ostrosłupa prawidłowego czworokątnego , którego krawędź podstawy ma długość a, a krawędź boczna b..

Ekspresowy Kurs Maturalny z matematyki

Nadesłane rozwiązania ( 1 )

Znasz inny sposób na rozwiązanie tego zadania?

Dodaj swoje rozwiązanie: