Spośród wierzchołków sześcianu ABCDEFGH wybrano trzy. Oblicz prawdopodobieństwo zdarzenia polegające na tym, że wybrane wierzchołki sześcianu są wierzchołkami trójkąta różnobocznego.

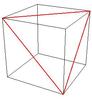
W załączniku przedstawiam jak to powinno wyglądać.

Ogólnie rzecz biorąc trzy dowolne wierzchołki możemy wybrać na sposobów.

Teraz rozważmy wybór takich wierzchołków, które utworzą trójkąt równoboczny. Otóż długość boku tego trójkąta musi być równa przekątnej kwadratu (patrz rysunek).

Pierwszy wierzchołek wybieramy dowolnie, a więc na sposobów. Drugi wierzchołek musi być przeciwległym wierzchołkiem w sąsiadującej ścianie, a więc sposoby. Trzeci wierzchołek też musi być przeciwległym wierzchołkiem sąsiadującej ściany, ale zostały już tylko dwie opcje.

Zatem szukane prawdopodobieństwo wynosi:
\frac{8\cdot 3\cdot 2}{8\cdot 7\cdot 6}=\frac{1}{7}

w zadaniu jest mowa o trójkącie róŻnobocznym a wiec zadanie jest zle wykonane, prawidłowa odp to 3/7.