Zadanie
dodane przez
spajsy34
,
03.04.2013 15:27
Rzucamy trzy razy sześcienną kostką do gry . Wśród podanych zdarzeń wskaż zdarzenie pewne . A.iloczyn wyrzuconych oczek jest liczbą parzystą B. suma wyrzuconych oczek wynosi conajmiej 3 . C. w trzecim rzucie wypadną conajmiej trzy oczka D. trzykrotnie wypadnie ta sama liczba oczek .
Nadesłane rozwiązania ( 2 )
Rozwiązanie 1
dodane przez
kasienka1813
,
03.04.2013 16:19
zdarzenie pewne=  =216
=216
A. 216:2=108 przypadków liczb parzystych
czyli P(a)= =
=
B. suma ma wynosić conajmniej 3. Czyli 3 i więcej. Czyli są to wszystkie przypadki
P(a)= =1
=1
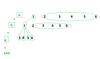
C. patrz rysunek :
mnożymy ilość przypadków : 4*6*6=144
P(a)= =
=
D. takich przypadków mamy 6:
1,1,1
2,2,2
3,3,3
4,4,4
5,5,5
6,6,6
P(a)= =
=
 =216
=216
A. 216:2=108 przypadków liczb parzystych
czyli P(a)=
 =
=
B. suma ma wynosić conajmniej 3. Czyli 3 i więcej. Czyli są to wszystkie przypadki
P(a)=
 =1
=1
C. patrz rysunek :
mnożymy ilość przypadków : 4*6*6=144
P(a)=
 =
=
D. takich przypadków mamy 6:
1,1,1
2,2,2
3,3,3
4,4,4
5,5,5
6,6,6
P(a)=
 =
=
-
- Dodaj komentarz
Musisz się
zalogować
aby dodać komentarz
Rozwiązanie 2
dodane przez
kasienka1813
,
03.04.2013 16:21
zdarzenie pewne=  =216
=216
A. 216:2=108 przypadków liczb parzystych
czyli P(a)= =
=
B. suma ma wynosić conajmniej 3. Czyli 3 i więcej. Czyli są to wszystkie przypadki
P(a)= =1
=1
C. patrz rysunek :
mnożymy ilość przypadków : 4*6*6=144
P(a)= =
=
D. takich przypadków mamy 6:
1,1,1
2,2,2
3,3,3
4,4,4
5,5,5
6,6,6
P(a)= =
=
 =216
=216
A. 216:2=108 przypadków liczb parzystych
czyli P(a)=
 =
=
B. suma ma wynosić conajmniej 3. Czyli 3 i więcej. Czyli są to wszystkie przypadki
P(a)=
 =1
=1
C. patrz rysunek :
mnożymy ilość przypadków : 4*6*6=144
P(a)=
 =
=
D. takich przypadków mamy 6:
1,1,1
2,2,2
3,3,3
4,4,4
5,5,5
6,6,6
P(a)=
 =
=
Musisz się
zalogować
aby dodać komentarz


COMMENT_CONTENT