Zadanie
dodane przez
truskaawkowa
,
07.02.2013 20:18
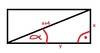
1. Przekatna prostokąta jest nachylona do dłuższego boku pod kątem L takim że sin=2/3 . Przekątna jest dłuższa od szerokości prostokąta o 4. Oblicz tg L oraz obwód tego prostokąta
Nadesłane rozwiązania ( 1 )
Rozwiązanie 1
dodane przez
Science4U
,
08.02.2013 11:30
W załączniku znajduje się odpowiedni rysunek.




Zatem przekątna ma długość
 .
.
Z twierdzenie Pitagorasa mamy:




Tangens:

Obwód:

-
- Dodaj komentarz
Musisz się
zalogować
aby dodać komentarz


COMMENT_CONTENT