Wybierz dział:
Trapez ABCF jest podobny do trapezu FCDE. Oblicz długość ED.
Odcinki AB i CD są równoległe. Oblicz x.
Kąt środkowy i kąt wpisany są oparte na tym samym łuku.Suma ich miar jest równa 300 stopni. Jaka jest miara kąta wpisanego?
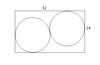
W prostokąt o bokach długości 24 i 32 wpisano w sposób pokazany na rysunku dwa styczne okręgi o równych promieniach. Oblicz długość promieni okręgów.
Dany jest trójkąt równoboczny o boku 18cm.Oblicz pole tego trójkąta ,promień okręgu wpisanego w ten trójkąt oraz pole koła opisanego na tym trójkącie
Punkty A=(3,1), B=(7,3) są kolejnymi wierzchołkami kwadratu ABCD. Wyznacz współrzędne wierzchołka C tego kwadratu.
Promień okręgu wpisanego w trapez wynosi 6. Długość odcinka łączącego środki ramion jest równa 8. Oblicz pole tego trapezu.
Kąt ostry równoległoboku ma miarę, przekątne tego równoległoboku mają długości 3,5 cm i 0,5
cm. Wyznacz długości boków równoległoboku.
Środkowe poprowadzone z wierzchołków kątów ostrych trójkąta prostokątnego mają długości 2 i 3. Znajdź pole tego trójkąta.
Promień koła wpisanego w trójkąt prostokątny równa się 1. Punkt styczności tego okręgu z przeciwprostokątną dzieli ją na dwa odcinki, których stosunek równa się 2:1. Oblicz pole i obwód tego trójkąta.
oblicz pola. zadania w kółku w załączniku
Dany jest równoległobok ABCD. Przez wierzchołek D poprowadzić: a) dwie proste, b) cztery proste, dzielące dany równoległobok na części o równych polach. ( analiza, konstrukcja, dowód). Bardzo bym prosiła o jakąkolwiek pomoc, jakieś wskazówki jak zrobić to zadanie. Z góry dziękuję - ula.
W sześcian o krawędzi a wpisano ośmiościan foremny tak, że wierzchołki ośmiościanu znajdują sie w środkach ścian sześcianu. Oblicz objętość i pole powierzchni ośmiościanu. Oblicz stosunek objętości ośmiościanu do jego pola
Dany jest czworokąt ABCD, w którym AB || CD. Na boku BC wybrano taki punkt E, że | EC| = |CD| i |EB| = |BA|. Wykaż, że kąt AED jest prosty.
W trójkącie ABC długości boków są równe: I AC I =50 a I AB I =7 a kąt między nimi zawarty na miarę 123stopni .Oblicz pole i obwód trójkąta.wypisz dane,szukane i sformułuj odpowiedz do tego zadania.
Hej, nie jest to zadanie do końca, jednak nikt nie potrafi mi odpowiedź na pytanie. Brzmi ono tak: cechy przystawania trojkątów to bok-bok-bok, bok-kąt-bok i kąt-bok-kąt. Cechy podobieństwa trójkątów to to samo tylko zamiast kąt-bok-kąt jest kąt-kąt-kąt. Czy ktoś mi może wytłumaczyc, dlaczego zasada kąt bok kąt nie stosowana jest do podobieństwa. Ostatnio robiłam zadanie w którym trzeba było z tego skorzystac i oczywiście nie wykorzystałam tej nieistniejącej zależności. Jednak gdyby namalowac dwa trójkąty w skali 1:2 i odpowiednio miałyby długosc boku tą samą i kąty miedzy nimi, to dla mnie po przeciągnięciu z tych kątów boków odpowiednio i trzeciego wyjdzie mi zasada kąt-bok-kąt, Ktokolwiek, help?
a) Pole rombu jest równe 48cm2, a krótsza przekątna ma długość 8cm. Oblicz obwód tego rombu.
b) Bok rombu ma długość 8, a kąt ostry ma miarę 60stopni . Oblicz wysokość tego rombu.
Ile punktów wspólnych ma okrąg o równaniu (x+2)^2+(y – 1)^2=9
a) z osią OX
b) z prostą y = - 2.
Promień okręgu wpisanego w trójkąt równoboczny jest równy 2. Oblicz obwód tego trójkąta.
W okrąg wpisany jest kąt BAC równy 280. Przez punkt C poprowadzono styczną do tego okręgu Oblicz miarę kąta ostrego między tą styczną a cięciwą AC.
Kąt środkowy i kąt wpisany są oparte na tym samym łuku. Suma ich miar jest równa 2200. Oblicz miarę kąta środkowego.
Wykaż, że odcinek x łączący środki ramion trapezu o podstawach a, b ma długości
Dany jest trapez równoramienny o podstawach |AB| = a, |DC| = b (a>b). Odcinek DE jest wysokością tego trapezu. Wykaż, że |EB| =
Dany jest trójkąt prostokątny ABC o przyprostokątnych AC, BC. Odcinek CD jest wysokością trójkąta, kąt CAB =, a punkt O jest środkiem okręgu opisanego na trójkącie. Wyznacz miarę kąta DCO.
Dany jest trójkąt równoramienny ABC o ramionach AC, BC i podstawie AB. Na prostej AB zaznaczono na zewnątrz trójkąta punkty E, F, takie, że |AE| = |BF|. Wykaż, że trójkąt EFC jest równoramienny.
i przy okazji chciałabym prosić o jakieś proste takie nie skomplikowane wytłumaczenie o co chodzi w tym podobieństwie bbb lub bkb lub kkk, bo często się zdarza w tego typu zadaniach a ja nie wiem jak ocenić, którą z tych cech trzeba wybrać