Wybierz dział:
Proszę o pomoc
W pewnym trójkącie prostokątnym boki mają długosci 3cm, 4cm i 5cm. W trójkącie podobnym do niego najdłuższy bok ma długosc 2,5cm. Pole tego drugiego trójkata jest równe:
a).1,5cm do kwadratu
b).3cm do kwadratu
c).6 cm do kwadratu
d).9 cm do kwadratu
Bardzo dziękuję
Wewnątrz danego kąta ostrego obrano dwa różne punkty P i Q. Zbuduj równoległobok, którego dwoma przeciwległymi wierzchołkami są punkty P i Q a pozostałe dwa leżą na ramionach kąta. Proszę o rysunek.
W trójkącie ABC : XY II BC . Wiedząc , że pole trójkąta AYX jest równe 4 cm^2 , wyznacz :
a) pole trójkąta ABC,
b) pole czworokąta XYBC,
W trapezie ABCD : AB II CD oraz przekątne AC i BD przecinają się w punkcie P. Wyznacz długość odcinka PC, jeśli stosunek pola trójkąta CDP do pola trójkąta ABP wynosi 16:25 i odcinek AP ma 8 m długości.
Długości trzech kolejnych boków czworokąta opisanego na okręgu są kolejnymi liczbami naturalnymi.Obwód czworokąta wynosi 36 cm.Oblicz długości jego boków.(odpowiedź do tego zadania to 8,9,10,9)
Wykaż , że jeśli w równoległobok można wpisać okrąg , to jest on rombem.
Ramię trójkąta równoramiennego ma długość 12 i tworzy z podstawą kąt o mierze 45 stopni.Z wierzchołka tego trójkąta poprowadzono do podstawy odcinek dzielący kąt przy wierzchołku w stosunku 2:1. Oblicz pola powstałych trójkątów.
oblicz pole kola opisanego na szesciokacie foremnym jezeli wiesz ze pole kola wpisanego w ten szesciokat jest rowne S.
W kwadrat wpisano kolo a nastepnie w to kolo wpisano kwadrat. Roznica pol tych kwadratow jest rowna 8 c. Oblicz pole kola.
Prostokąt P1 ma boki długości 12cm i 16 cm. Prostokąt P2 ma przekątną długości 25cm i jeden z boków długości 20 cm. Uzasadnij, że prostokąty te są podobne i podaj ich skale podobieństwa.
Udowodnij, że jeżeli trapez ma przekątne równej długości to jest równoramienny.
Dane są dwa okręgi o promieniach 12 i 17. Mniejszy okrąg przechodzi przez środek większego okręgu. Odległość między środkami tych okręgów jest równa:
A,5 B.12 C.17 D.29
Dany jest trójkąt prostokątny i przyprostokątnych 5 i 12. Promień okręgu opisanego na tym trójkącie jest równy:
A.12 B.8.5 C.6.5 D.5
a)Odległość między miastami A i B na mapie sporządzonej w skali 1: 2 500 000 jest równa 3cm. Oblicz rzeczywistą odległość między tymi miastami.
b)Odległość między miastami A i B na mapie wynosi 4cm, natomiast odległość rzeczywista między tymi miastami jest równa 8km. Oblicz w jakiej skali została sporządzona mapa.
c)Rzeczywista odległość między miastami A i B wynosi 40km. Oblicz odległość między tymi miastami na mapie sporządzonej w skali 1: 200 000.
Dane są dwa współśrodkowe koła o promieniach 5cm oraz 8cm. Oblicz:
a)Pole pierścienia utworzonego przez te dwa koła;
b)długość odcinka, który jest cięciwą większego koła i jednocześnie jest styczny do mniejszego koła;
c)jaki procent obwodu większego koła stanowi obwód mniejszego koła.
W wyniku kołowym o promieniu 3cm, kąt środkowy ma miarę. Oblicz:
a)pole tego wycinka koła;
b)obwód tego wycinka koła;
c)pole koła wpisanego w ten wycinek koła.
Dany jest trójkąt o bokach:3,
6,
12. Uzasadnij że:
a)obwód tego trójkąta jest równy 3(3+1);
b)długości boków tego trójkąta są trzema kolejnymi wyrazami ciągu arytmetycznego.
W trójkącie równoramiennym ramiona są długościcm, a kąt między tymi ramionami ma miarę
.Oblicz:
a)Pole tego trójkąta;
b)Pole koła wpisanego w ten trójkąt;
c)Pole koła opisanego na tym trójkącie.
Dany jest trójkąt prostokątny o przyprostokątnych długości 4cm icm. Oblicz:
a)wysokość tego trójkąta poprowadzoną do przeciwprostokątnej;
b)promień okręgu wpisanego w ten trójkąt;
c)długość odcinków, na jakie wysokość prowadzona z wierzchołka kąta prostego podzieliła przeciwprostokątną.
Dany jest trójkąt równoboczny o boku długości.Oblicz:
a)wysokość tego trójkąta;
b)promień koła wpisanego w ten trójkąt;
c)stosunek pola koła opisanego na tym trójkącie, do pola koła wpisanego w ten trójkąt.
srednia arytmetyczna cen sześciu akcji na giełdzie jest równa 500 zł . za pięć z tych akcji zapłacono 2300 zł. cena szóstej akcji jet równa ?
flagę tak jak pokazano na rys , należy zszyć z trzech jednakowej szerokości pasów kolorowej tkaniny . oba pasy zewnętrzne mają być tego samego koloru , a pas znajdujący się między nimi ma być innego koloru. liczba różnych takich flag , które można uszyć , mając do dyspozycji tkaniny w 10 kolorach , jest równa ?
narysowana jest flaga czerwona biało czerwona .
Bok rombu ma dł.6cm a jego kat ostry rozwarty ma miarę 150stopni oblicz pole rabu
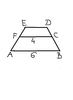
Trapez ABCF jest podobny do trapezu FCDE. oblicz długość ED.
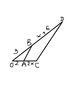
Odcinki AB i CD są równoległe. Oblicz x.